Please clear all the concept step by step for dome calculation, arc length, volume
- Thread starter javed746
- Start date
Dnyan Deshmukh
Staff member
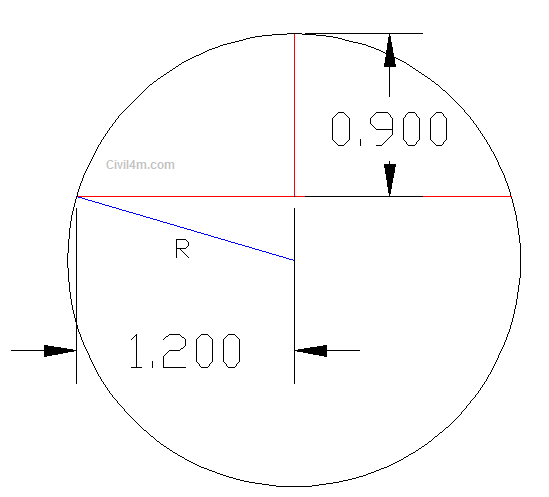
This is recreated in Auto Cad as per details given by you
Your question is very nice and interesting.
First of all we need to find the radius of this spherical dome.
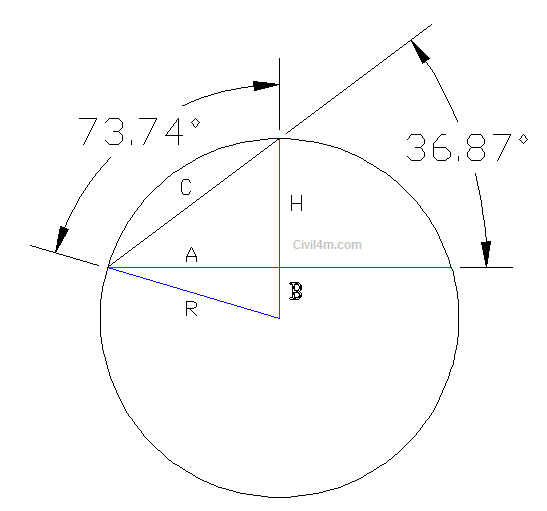
To find a radius, take a look at triangle formed by lines A,B and R.
Use a theorem,
R^2 = A^2 + B^2
Hear we can take B as, (R-H)
R^2 = A^2 + (R-H)^2
Remembered below formula
(A-B)^2 = A^2 - 2AB + B^2
So here we get,
R^2 = A^2 + R^2 – 2RH + H^2
R^2 - R^2 + 2RH = A^2 + H^2
2RH = A^2 + H^2
R = ( A^2 + H^2) / 2H
The above equation will help to find the radius of dome.
So radius is Equal
R = ( 1.22 + 0.92) / 2 x 0.9
R = 1.25 Meter.
What is Perimeter of Circle?
2∏R x angle in degree /360
angle of Circle is 360 so perimeter will become
2 x Pi x R or 2∏R
As the arc is not a full circle, to find the perimeter, we need to find the angle of arc.
There is relation between the angles, angle between line B and R is double than the angle between line A and C.
As this angle cuts arc at center, the angle of arc will be double of angle between line B and R.
Find the angle between line A and C
tan Ф = H / A
Ф = tan-1 (H / A)
Ф = tan-1 (0.9 / 1.2)
Ф = 36.87
So the angle between line B and R will be = 2 x 36.87 = 73.74
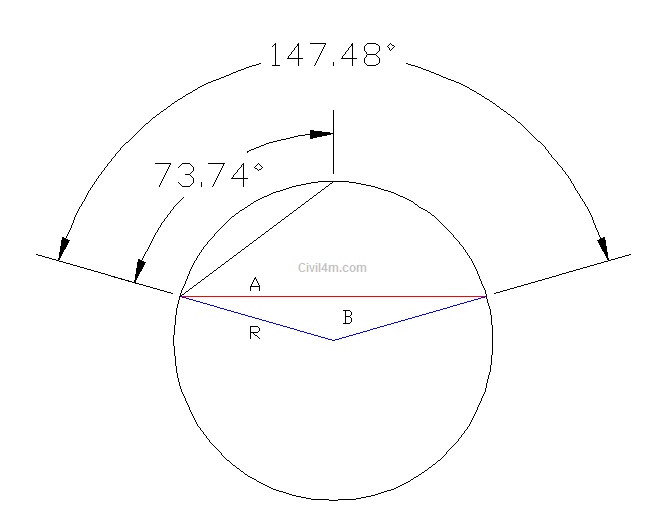Hence the angle of complete arc will be = 2 x 73.74 = 147.48
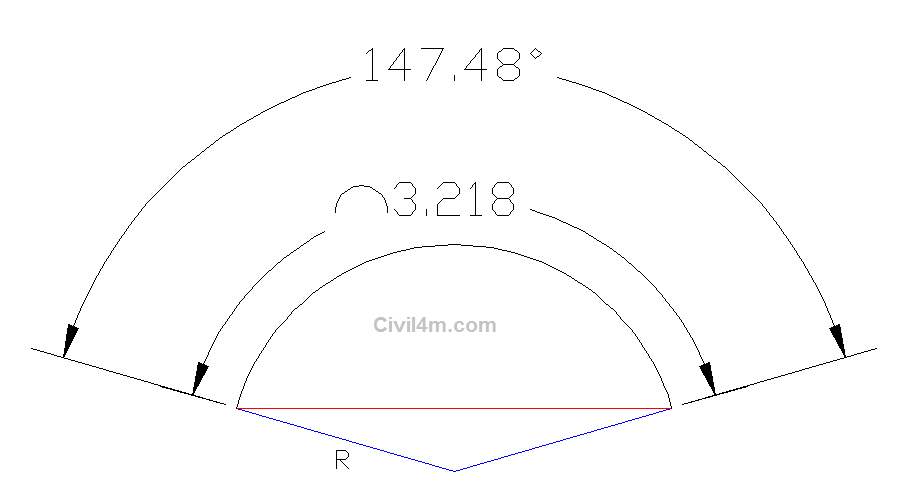
Now we have radius of dome and the angle of arc from center of sphere.
The perimeter or the length of the arc = 2∏R x (Ф/360)
= 2 x 3.14 x 1.25 x (147.48/360)
= 3.216 Meter
The formula for the surface area of dome is
2∏RH
So the surface area of dome is = 2 x 3.14 x 1.25 x 0.9
= 7.065 Sqm
The thickness of the dome is 150 mm so approx volume will be = 7.065 x 0.15 = 1.06 Cum
All results are verified in auto cad and have minor difference due to calculations by taking decimals into consideration.
